
The views expressed are those of the author(s) and are not necessarily those of Scientific American. For example, What are Prime numbers between 20 and 30 Select the initial number (e.g. But hey, the silver lining would be that we might actually gain some insight into prime numbers as a result! This calculator will show a list of primes between the given numbers. On the other hand, wouldn’t it be funny if somehow we could figure out that the sequence did not contain all prime numbers, but we couldn’t figure out which ones never showed up? The least amusing option, I suppose, would be for someone to figure out a simple rule that would determine whether a number was in the Euclid-Mullin sequence or not.

HRABDWEFXLMNSIJGKQOPCTVYUZ (phonetic spellings being somewhat debatable, your mileage may vary). It would be like putting the letters of the alphabet in the alphabetical order of their phonetic spellings: I love the fact that it would give us a new natural order to put the prime numbers in. I am drawn to adorable and amusing math, so I hope the Euclid-Mullin sequence contains all prime numbers. If the Euclid-Mullin sequence does avoid some primes, why? And could we look at a prime and tell whether it is in the sequence or not? The similar sequence that chooses the largest instead of smallest prime that divides 1 plus the product of the previous terms avoids an infinite number of primes. The smallest prime not known to appear on the list is 41. We do not know whether every prime number appears in the Euclid-Mullin sequence. The seventh term is the number 5, but the ninth term has 14 digits! Finding the 52nd term of the sequence requires the factorization of a 335-digit number. As the number of terms grows, we run into very large numbers that take a long time to factor, in part because the sequence bounces around a lot. The sequence has infinitely many terms, but we know only 51 of them. Ken Ribet mentioned the Euclid-Mullin sequence when my cohost Kevin Knudson and I talked with him for our podcast My Favorite Theorem, and it’s been rattling around in my brain ever since. If you know of a term named for people who lived more than 2200 or so years apart from each other, let me know on Twitter.) (Side question: Is the Euclid-Mullin sequence the poly-eponymous term in math with the greatest chronological gap between eponyms? Euclid, or the person or group of people who wrote Euclid’s Elements, lived around 300 BCE in Alexandria American mathematician and engineer Albert Mullin was born in 1933 and died in 2017. It is sequence A000945 in the Online Encyclopedia of Integer Sequences. The Euclid-Mullin sequence is the sequence that starts 2, 3, 7, 43, 13, and so on: the first term is 2, and each subsequent term is the smallest prime factor of 1 plus the product of all previous terms. To find the next number, we multiply 2×3 and add 1 to get 7, which is prime. The first one is easy: 2+1=3, and 3 is prime.

To see why, we can start thinking about what numbers we would get if we started with the first prime, 2, and used it to find new primes using the process from Euclid’s proof. Hence, the finite list of primes is incomplete.Ī common misconception about this proof is that the number p 1×p 2×p 3×…×p n +1 itself has to be prime. This number, p 1×p 2×p 3×…×p n +1, is not divisible by any of the primes on our list the remainder when we divide it by one of those primes is 1. If your primes are p 1, p 2, p 3,…,p n, take the product of all of them: p 1×p 2×p 3×…×p n and add 1. Before I show you the list, here's how to generate a list of prime numbers of your own using a few popular languages. I assembled this list for my own uses as a programmer, and wanted to share it with you. One of the first questions a curious human could ask about prime numbers is how many there are, and one of the earliest proofs that there are infinitely many primes is a lovely argument from Euclid’s Elements.Įuclid’s proof starts with a finite list of prime numbers and describes a way to generate a prime that is not on the list. Prime Numbers List A Chart of All Primes Up to 20,000 Quincy Larson Here's a list of all 2,262 prime numbers between zero and 20,000.
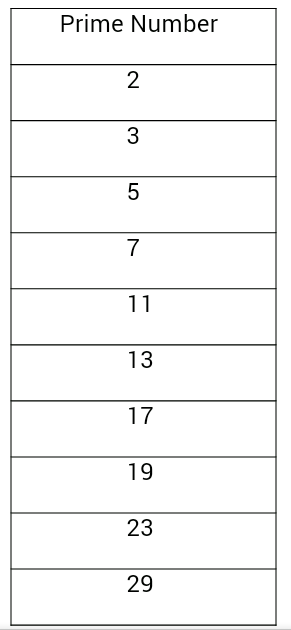
(Hence 1 is not considered a prime number.) All whole numbers greater than 1 are either primes or products of primes. A prime has exactly two distinct factors: itself and 1. If the division of counter by any value of lower does not produce a remainder, then counter is not a prime number.Į.g.Prime numbers are often described as the “atoms” of mathematics, or at least of numbers. Note that % is modulo which returns the remainder of a division. It looks like: for (begin repeat-condition update) The for loop uses a numeric counter to keep score of how many times an action has to be repeated. It reads like: while, do somethingįor our tinko-tinko game, this would be: while no player has faltered, do hand movement For Loop

In fact, the while loop is perhaps the perfect kind of loop for this. Such a game is a classic example of a loop. The game would be played by repeating the hand movements till someone falters.


 0 kommentar(er)
0 kommentar(er)
